Here are their names and numerals. The Powers of 10 | Class of | One | 1 | | Ones | Ten | 10 |
| One hundred | 100 | | | | Class of | One thousand | 1,000 | | Thousands | Ten thousand | 10,000 | | | One hundred thousand | 100,000 | | | | Class of | One million | 1,000,000 | | Millions | Ten million | 10,000,000 | | | One hundred million | 100,000,000 | | | | Class of | One billion | 1,000,000,000 | | Billions | Ten billion | 10,000,000,000 | | | One hundred billion | 100,000,000,000 |
Each power is composed of ten of the one above. (The metric system is the system of measurement based on the powers of 10; see Lesson 4.) Strictly, 1 is not a power of 10. The first power of 10 is 10 itself. Its numeral is a 1 followed by one 0. The second power of 10 is 100; it has two 0's. The third power has three 0's. And so on. Notice how the names fall into groups of three: One thousand, Ten thousand, Hundred thousand. One million, Ten million, Hundred million. Each group of three -- Ones, Tens, Hundreds -- is called a class. |
Example 1. Read this number: 256,312,785,649,408,163 Answer. Starting from the left, 256, read each three-digit group. Then say the name of the class. 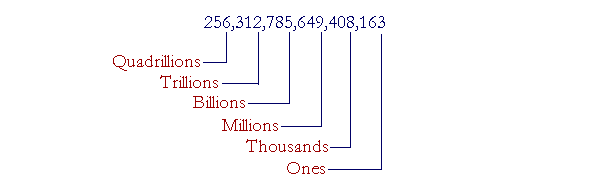 Say: "256 Quadrillion, 312 Trillion, 785 Billion, 649 Million, 408 Thousand, 163." Do not say the class name "Ones." Example 2. To distinguish the classes, place commas in this number: 8792456 Answer. Starting from the right, place commas every three digits: 8,792,456 Read the number: "8 million, 792 thousand, 456." Example 3. Read this number: 7,000,020,002 Answer. "Seven billion , twenty thousand, two." When a class is absent, we do not say its name; we do not say, "Seven billion, no million, ..." Also, every class has three digits and so we must distinguish the following: | 002 | "Two" | | 020 | "Twenty" | | 200 | "Two hundred" |
As for "and," in speech it is common to say "Six hundred and nine," but in writing we should reserve "and" for the decimal point, as we will see in the next Lesson. (For example, we should write $609.50 as "Six hundred nine dollars and fifty cents." Not "Six hundred and nine dollars.") Example 4. Write in numerals: Four hundred eight million, twenty-nine thousand, three hundred fifty-six. Answer. Pick out the classes: "million", "thousand". Each class (except perhaps the first class on the left) has exactly three digits: 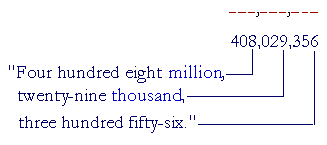
Example 5. Write in numerals: Five billion, sixteen thousand, nine. Answer. After the billions, we expect the millions, but it is absent. Therefore write 5,000,016,009 Again, we must write "sixteen thousand" as 016; and "nine" as 009; because each class must have three digits. The exception is the class on the extreme left. We may write "Five" as 5 rather than 005. When writing a four-digit number, such as Four thousand five hundred, it is permissible to omit the comma and write 4500. In fact, we often read that as "Forty-five hundred." But when a number has more than four digits, then for the sake of clarity we should always place the commas. Example 6. Distinguish the following: | a) Two hundred seventeen million | b) Two hundred million seventeen | | | | Answers. | | a) 217,000,000 | b) 200,000,017 |
| 5. | To which place does each digit belong? Equivalently, what is the unit at each position? | | | 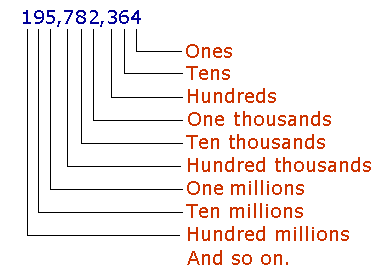 | | | | | Starting with the Ones on the right, each place belongs to the next power of 10. | | |
| Example 1. In this number, 139,072,658 the 0 is in which place? Answer. Hundred thousands. For, in each class of three digits, there are Ones, Tens, and Hundreds. 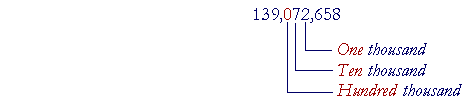 0 is in the class of thousands and in the Hundreds place. The power of 10 at that position is Hundred thousands. Example 2. In this number, 386,214,035 how many Ten millions are there? That is, which digit is in the ten millions place? Answer. 8. For, on counting from the right, the millions are the third group of three digits, 386. The Tens place is the middle one (Ones, Tens, Hundreds). There are 8 Ten millions. Place value versus absolute value of a digit In addition to speaking of a digit being "in" a place, we also speak of the place value of the digit itself. In this number, 6,666 each digit has the same absolute or invariable value 6, but a different place value. 6 on the extreme left has the place value 6000; the next 6 has the value 600; the next, 60; and the last, 6. Expanded form The numeral for every whole number stands for a sum. 364 = 3 Hundreds + 6 Tens + 4 Ones. (Even a single digit stand for a sum: 5 = 1 + 1 + 1 + 1 + 1.) What is written above is called the expanded form of 364. | | | | 6. | What does it mean to write a number in expanded form? | | | | | It means to write the sum that the number indicates, and therefore to name the unit at each digit's place. | | |
| Example 3. Write 6,325 in expanded form. Answer. Write 6,325 = 6 Thousands + 3 Hundreds + 2 Tens + 5 Ones. In practice, however, it is often more useful to expand the number in this way: 6,325 = 6,000 + 300 + 20 + 5. Example 4. Write the expanded form of 10,000. Answer. 10,000 = 1 Ten-thousand + 0 Thousands + 0 Hundreds + 0 Tens + 0 Ones. | | | Example 5. | | 42 | = | 40 + 2 | | | | -- no matter what the unit. | | | | | 42 eggs | = | 40 eggs + 2 eggs | | | | | 42 tens | = | 40 tens + 2 tens | | | | | 42 hundreds | = | 40 hundreds + 2 hundreds |
And so on. For there is no "42" apart from 42 units, even though we do not say the word units. Units of adjacent place value The following question is to prepare for the standard written methods ofaddition and subtraction. The answer follows from the fact that each digit 6,325 has a place value ten times the digit to its right. For, each power of 10 is ten times the one to its right: 1000 100 10 1 1000 is made up of ten 100's. 100 is made up of ten 10's. 10 is made up of ten 1's. And so on. | | | | 7. | What is the relationship between units of adjacent place value? | | 1000 100 10 1 | | | Ten units of lower place value can be composed -- gathered together -- to make one unit of the next higher value. | | | | | Equivalently: One unit of higher place value can bedecomposed -- broken up -- into ten units of the next lower value. | | |
|

Ten 1's can be composed into one 10. Ten 10's can be composed into one 100. Ten 100's can be composed into one 1000. And so on. Conversely: 1000 100 10 1 One 1000 can be decomposed into ten 100's. One 100 can be decomposed into ten 10's. One 10 can be decomposed into ten 1's.  1000 100 10 1  We will see this when we come to regrouping in addition and subtraction. Rounding off | | 8. | How do we round off, or approximate, a whole number to a given place? | | | 1267 1300 1300 | | | | | Look at the digit to the right of the given place: hundreds for example (2). If the digit to the right is a 5 or greater, add 1 to the given place. If it is less than 5, leave the given place unchanged. In either case, replace all the digits to the right of the given place with 0's. | | |
| Example 6. Round off 6,528 to the nearest ten. Answer. 6,528 6,530 6,530 (The wavy equal sign means "is approximately equal to.") means "is approximately equal to.") 2 is in the tens place. To round off to the nearest ten, look at the digit to the right: 8 (greater than 5). Therefore, add 1 to the tens place. Replace 8 with 0. Example 7. Round off 6,528 to the nearest hundred. Answer. 6,528 6,500 6,500 5 is in the hundreds place. To round off to the nearest hundred, look at the digit to the right: 2 (less than 5). Therefore, leave the hundreds place unchanged. Replace 28 with 00. Example 8. Round off 6,528 to the nearest thousand. Answer. 6,528 7,000 7,000 6 is in the thousands place. To round off to the nearest thousand, look at the digit to the right: 5. Therefore, add 1 to the thousands place. Replace 528 with 000. Example 9. Round off 79,521 to the nearest thousand. Answer. 79,521 80,000 80,000 9 is in the thousands place. To round off to the nearest thousand, look at the digit to the right: 5. Therefore, add 1 to 79 -- it becomes 80. Replace 521 with 000.
| 9. | How do we multiply a whole number by a power
of 10? | | 28 × 10 | | | | | Add on as many 0's as appear in the power. | | |
|
| Example 1. | 28 × 10 | = | 280 | | Add on one 0. | | | | | 28 × 100 | = | 2800 | | Add on two 0's. | | | | | 28 × 1000 | = | 28,000 | | Add on three 0's. |
We can do that because of our system of positional numeration.
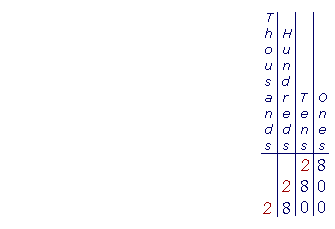 Look at 28 in the figure, and let us push each digit one place left, so that it becomes 280. 280 is then ten times 28, because each digit's place value is now ten times more. (In 28, the '2' tells how many tens, but in280 it tells how many hundreds.) Similarly, 2800 = 100 × 28.
Example 2. 608 is 608 ones. How much are 608 tens? 608 hundreds? 608 thousands? Answers. "608 tens" is 608 × 10. That is the meaning of multiplication (Lesson 9). 608 tens therefore are 6,080. Simply add on a 0. 608 hundreds = 608 × 100 = 60,800. Add on two 0's. 608 thousands = 608 × 1000 = 608,000. Add on three 0's.
Example 3. a) 50 ones are equal to how many tens? Answer. 50 ones are simply 50, or 5 tens. b) 50 tens are how many hundreds? Answer. 50 tens = 500. (Add on a 0.) 50 tens are 5 hundreds. c) 50 hundreds are how many thousands? Answer. 50 hundreds = 5000. (Add on two 0's.) 50 hundreds are5 thousands. d) 5000 is how many tens? Answer. 5000 = 500 × 10. 5000 is 500 tens. | | 10. | When a whole number ends in 0's, how do we divide it by a power of 10? | | | | 42,000 ÷ 10 | | | | | Take off as many 0's as appear in the power. | | |
|
| Examples. | 42,000 ÷ 10 | = | 4,200 | Take off one 0. | | | | | 42,000 ÷ 100 | = | 420 | Take off two 0's. | | | | | 42,000 ÷ 1000 | = | 42 | Take off three 0's. |
Problem. Reduce this fraction to its lowest terms: Answer. To reduce a fraction, we must divide both the numerator and denominator by the same number. Now, if a number ends in 0, then we know that it is divisible by 10; while if a number ends in two 0's, we know that it is divisible by 100. Both 300 and 500 then are divisible by 100:
|
|
|